 La trigonometría es una rama de las matemáticas cuyo significado etimológico es “la mediciónde los triángulos“.
La trigonometría es una rama de las matemáticas cuyo significado etimológico es “la mediciónde los triángulos“.
En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión.
La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio. Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.
Definiciones básicas.

Funciones trigonométricas.
La trigonometría es el estudio de la relación entre los lados y los ángulos del triángulo rectángulo. Muchas aplicaciones de la trigonometría dependen de esta relación. A estas relaciones las denominamos funciones trigonométricas.
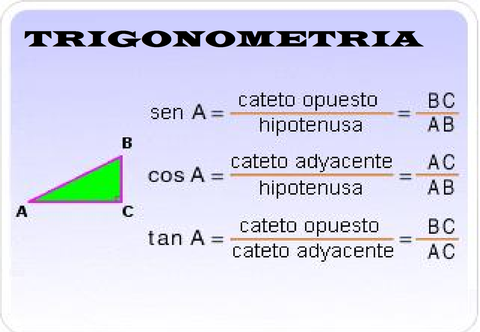
Sea el triángulo ABC un triángulo rectángulo con el ángulo recto en el vértice C.

Sus lados a y b son sus catetos y el lado c la hipotenusa. Cada ángulo, en el triángulo tiene un lado opuesto, lado de frente al ángulo, y un lado adyacente, lado que forma parte del ángulo en cuestión.
De la forma en que ha sido configurado el triángulo en este ejemplo, el vértice A tiene al cateto a como lado opuesto y al cateto b como lado adyacente.
De igual forma el vértice B tiene al cateto b como lado opuesto y al cateto a como lado adyacente. Los lados opuestos y adyacentes se intercambian entre sí para los dos ángulos que no son el ángulo recto en el triángulo rectángulo.
 En el caso del ángulo recto, hay que notar que tiene como lado opuesto a la hipotenusa y no tiene lado adyacente.
En el caso del ángulo recto, hay que notar que tiene como lado opuesto a la hipotenusa y no tiene lado adyacente.
El identificar los lados opuestos y adyacentes respecto a un ángulo es sumamente importante a la hora de definir las funciones trigonométricas.
En esta unidad solamente definiremos las tres funciones trigonométricas básicas: seno, coseno y tangente.
Estas son las convenientes y utilizadas en Física para resolver problemas.
Ejemplos.
Seno.
Se define la función seno (sen) de un ángulo como la proporción que existe entre el lado opuesto y la hipotenusa. Matemáticamente esta proporción se expresa como:

 Donde el símbolo θse utiliza para denotar el ángulo que estaremos considarando.Observa la figura de la izquierda. En ella hay un triángulo con unas cantidades medidas.
Donde el símbolo θse utiliza para denotar el ángulo que estaremos considarando.Observa la figura de la izquierda. En ella hay un triángulo con unas cantidades medidas.
Sea el ángulo igual a 30° y su lado opuesto igual a 5 cm y la hipotenusa igual a 10 cm, entonces el seno de 30° es:
El procedimiento para calcular el seno sería:

Los valores de las funciones trigonométricas no tienen unidades ya que se cancelan. También son independientes del tamaño del triángulo. El seno de 30° siempre es igual a 0.5.
El triángulo que mejor nos muestra esta relación es:

Coseno.
La función coseno (cos) se define como la proporción entre el lado adyacente y la hipotenusa. Esta función se expresa como:

Sea el ángulo igual a 45° y su lado opuesto igual a 7 cm y la hipotenusa igual a 10 cm, entonces el coseno de 45° es:


Puedes notar que se utilizó la función de

esta se lee “coseno inverso” pero su significado es el el recíproco de la función lo cual representa un número que nos da el ángulo correspondiente. Puedes usar la calculadora para obtener el resultado. El triángulo básico que mejor nos muestra esta relación es:

Tangente.
La función tangente se define como la proporción entre el lado opuesto y el adyacente. Esta función se expresa como:

Sea el ángulo igual a 60° y su lado opuesto igual a 8 cm y el adyacente igual a 4.62 cm, entonces la tangente de 60° es:


Puedes usar la calculadora para revisar los cálculos aquí demostrados y sustituir otras cantidades en los ejemplos demostrados. El mejor triángulo que representa la situación del ejemplo es:


