 Un vector es una herramienta utilizada en geometría a la hora de representar una determinada magnitud física. Se trata de segmentos de rectas que se forman a partir de un determinado punto en el espacio y que poseen cierta dirección, magnitud y sentido. Este se usa para representar cierta magnitud física, donde llega a estar bien definido por una dirección, un módulo y una orientación.
Un vector es una herramienta utilizada en geometría a la hora de representar una determinada magnitud física. Se trata de segmentos de rectas que se forman a partir de un determinado punto en el espacio y que poseen cierta dirección, magnitud y sentido. Este se usa para representar cierta magnitud física, donde llega a estar bien definido por una dirección, un módulo y una orientación.
Según la dirección que marquen, estos pueden ser positivos o negativos. Estos llegan a representar propiedades tanto en la suma como en la multiplicación de estos, donde cada uno muestra características diferentes.
Fuera del ámbito geométrico, también se nombra como vector a aquel agente que llega a transportar algo desde un lugar a otro. En biología llega a ser ese agente infeccioso que transmite una enfermedad de un individuo a otro.
Indice
¿Cuáles son las propiedades de los vectores?
Propiedades de los vectores para la suma
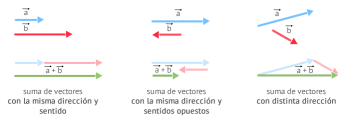 Propiedad conmutativa: indica que no importa el orden en que los vectores se sumen su resultado es el mismo, o sea, que la suma de un vector u con un vector v, será igual que la suma del vector c con el vector u.
Propiedad conmutativa: indica que no importa el orden en que los vectores se sumen su resultado es el mismo, o sea, que la suma de un vector u con un vector v, será igual que la suma del vector c con el vector u.- Propiedad asociativa: establece que no importa la forma en que se agrupen los vectores a la hora de sumar. Ejemplo: vector u + (vector v + vector w)= vector v + (vector w + vector u).
- Propiedad de identidad: también se le conoce como propiedad del elemento neutro. Indica que hay un vector que llega a funcionar como un elemento neutro al momento en que un vector cualquiera se le sume a él, donde el resultado siempre será el mismo vector original. En pocas palabras esta propiedad establece que la suma de todo vector con 0 siempre dará el vector original. Por ejemplo u + o = u. También indica que la suma de un vector por su opuesto dará como resultado 0. Ejemplo: u + (-u) = 0.
Propiedades de los vectores para la multiplicación
- Propiedad distributiva: esta llega a establecer que el resultado al multiplicar un vector independiente con otro que esté entre paréntesis es lo mismo que multiplicarlo ambos juntos. Ejemplo: c (u) = cu. Del mismo modo indica que el producto al multiplicar un vector por la suma de dos vectores que entren entre paréntesis, será lo mismo que multiplicar dicho vector por cada uno de los vectores que se estén sumando, y luego realizar la adición. Ejemplo: c (u + v) = cu + cv.
- Propiedad asociativa: indica que el resultado al multiplicar los vectores c y d por el vector u, siempre será igual que la multiplicación del vector c por el producto entre el vector d y u. También da el mismo producto si se multiplica el vector d por el producto entre los vectores c y u. Ejemplo: (cd) u = c (du) = d (cu).
- Propiedad de identidad: establece que el resultado al multiplicar un vector u por 1 siempre dará el mismo vector u. Ejemplo: 1 (u) = u.
Otras propiedades de los vectores
Origen
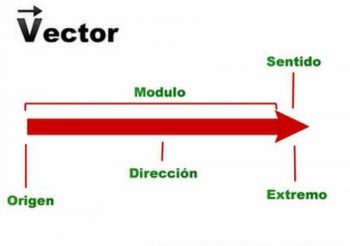 También se le conoce como punto de aplicación. Se trata del punto con exactitud en donde el vector llega a actuar.
También se le conoce como punto de aplicación. Se trata del punto con exactitud en donde el vector llega a actuar.
Dirección
Representa la orientación en el espacio de la recta que lo posee.
Módulo
Representa el tamaño o la longitud del vector. Para calcularlo se ha de tener el conocimiento sobre el origen o su punto de aplicación y del extremo del vector, luego se deberá de medir este origen hasta su extremo.
Sentido
Este llega a indicar a través de una punta de flecha que se coloca en el extremo del vector, la dirección hacia donde el vector se dirige con relación a la línea de acción.

